HOYA 灯管 200MXY 现货300 美萨全系列代理

1. 屈折率*

折射率是以真空（实际使用的是空气）中的光的相位速度与媒质中的光的相位速度的比来表示。

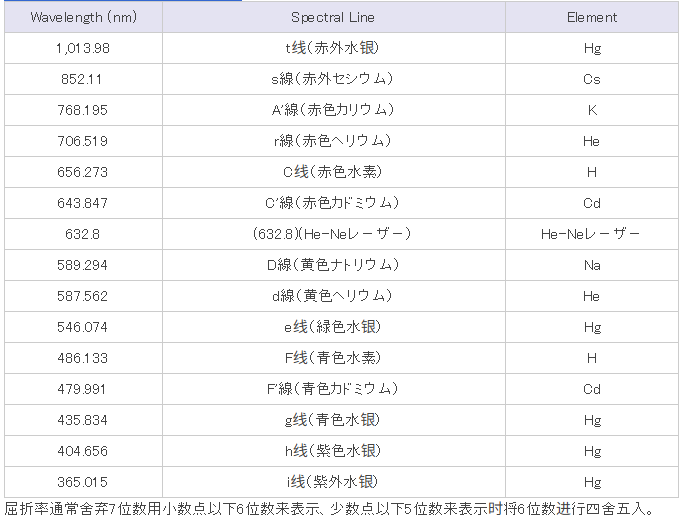
光学玻璃的折射率用以下15种光谱线测定表2所示。

表2 屈折率测定光谱线的波长和光源

2. 分布式

可使用对任意的波长 λ 之折射率 n 计算分布式。

n2 ＝ Ａ0+Ａ1λ2＋Ａ2λ-2＋Ａ3λ-4＋Ａ4λ-6＋Ａ5λ-8

这里的波长 λ是用μm単位表示。

用A0，A 1，A 2，A 3，A 4及A5硝种定为常数、以最小二乗法算出之値记载。

根据利用上式的常数、可计算出波长365~1014nm范围的任意波长之折射率公差精度±5×10-6。

分散常数的表示是用小数点以下的7位（把第8位四舍五入）记载表示。

3. 分散 *及以阿贝数*

色散是指折射率依存于光的波长的现象。 一般而言长波长光的折射率小于短波长光的折射率。

用阿贝数表示关于色散的性质的值、阿贝数νd 及νe分别用以下公式求得。

以小数点以下6位的数值表示主色散 nF - nC及nF'- nC 。 将以下3位数进行四舍五入用小数点以下2位数来表示，将以下4位数进行四舍五入用小数点以下3位数来表示。

4.部分分散比

部分色散比Px，y以及P'x，y分别用以下公式求得。

一般、部分色散比用任意光谱线间的计算值来表示。 在本产品目录中、使用频度高的Pd_c、Pg_F、P'd_c'、P' g_F'值来记载。 部分色散比用少数点以下6位数的屈折率来计算、将小数点以下5位数进行四舍五入、用少数点以下4位数来表示。

5. 异常分散性

纵轴表示部分分散比 Px，y 、横轴用阿贝数νd来表示的话、Px，y 于νd之间的好多硝材呈直线闰系、可以用近似公式来表示。 这里的x以及y表示光谱的种类。

Px，y = ax，y+bx，y・νd

这里ax，y以及bx，y为定数。 这样的硝种、被称为正常分散玻璃。 另一方面、离开正常分散玻璃的硝材被叫做异常分散玻璃、此种玻璃对缩小2次光谱非常有效。 距离正常分散玻璃的程度、也就是异常分散性的大小如果用ΔPx，y来表示的话、以上公式可以用更一般化的形式表示。

Px，y = ax，y+bx，y・νd+ΔPx，y

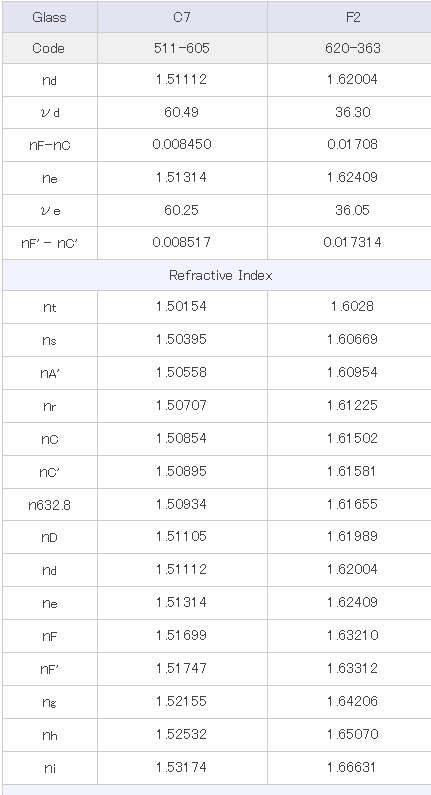
本手册中、通过正常分散玻璃基准的C7以及F2的坐标直线为标准线时、各个硝种的νd对应的标准线上的点与此硝种的Px，y的偏差用ΔPx，y 来表示。 ΔPx，y 方面，各硝种都记载了ΔPC_t、ΔPg_F 、以及ΔPi_g的数据。

表3 C7、F2的屈折率

6. 屈折率温度系数* （dn/dT）

光学玻璃的折射率随温度变化而变化。 绝对折射率的温度系数（Δn/ΔT）abs.是用干涉膨胀计在真空中测定试料温度变化而产生的光路长变化引发干涉条纹的移动量，和随膨胀而发生厚度变化的干涉条纹的移动量来求得。 （基于JOGIS18-1994）

以激光（波长：405、491、632.8、786nm）作为光源，在-40°C到150°C的温度范围内，

空気中（101.325kPa）における相対屈折率の温度系数每隔20°C测定一次数据。 空气中（101.325kPa）相对折射率的温度系数（Δn/ΔT）rel.用以下公式可以算出。

注 101.325kPa = 1atm

这里，Δnair. / ΔT为空气的折射率温度系数，在本手册中用左表来表示数据。

表4 空気的屈折率的温度系数

折射率温度系数的波长依存性

绝对折射率的温度系数与光的波长和温度的关系可以通过左边公式得出

  T0：Reference temperature (23℃)

  n(λ,Ｔ0)：Refractive index of light of wavelength λ at the reference temperature

  dnabs.(λ,Ｔ)/dT：Temperature coefficient of absolute refractive index of light of

           wavelength λ at temperature T

  ΔT：Temperature difference（T-T0)

D0， D1， D2， E0， E1，λ TK是硝种的固有恒数，在的Excel样册中有揭示。 另外，通过该公式计算得出的各波长，各温度的dn/dT也在的Excel样册中有揭示。

本样册中也揭示了通过nd的温度系数和nF及nC的温度系数得出的νd温度系数（dνd/dT）。

各温度时的膨胀系数

膨胀系数是表示高温域 300~100°C及低温域 -30~70°C的范围平均值，此次追加揭示了精细温度解析所需要的 -40~-20°C、20~40°C、80~100°C各热膨胀系数。

在中的Excel样册中将 -40~150°C的温域以20°C间隔进行揭示。

7. 光路长的温度系数（ds/dT）

当玻璃温度变化时光路长会有所变化。 这个变化程度

是以光路长的温度係数（ds/dT）表示。

这里的n是玻璃折射率、α是玻璃线膨张系数。 dn / dT是玻璃折射率的温度系数。

8. 光弹性定数 （ B）

光学玻璃通常经过严密的回火、在内部不会发生复折射。 但是如果机械外力作用于它、或加热、冷却造成有温度差时玻璃内部会产生应力、光学性能会发生改变、这样会造成复屈折性的发生。 复屈折的光路差δ（nm）、玻璃内部应力（差）σ（105Pa）、跟玻璃厚度d（cm）的关系为

δ = B・σ・t

上式的比例定数B为玻璃固有的定数、叫做光弹性定数、用10-12/Pa单位来表示。 本手册中使用He-Ne激光、在圆板状试料的一直线方向施加压缩荷重时、测定圆板中心产生的光路差、用此数据来计算光弹性定数。

Notes　

10-12 / Pa ＝ 0.9807(nm / cm) / (kgf / cm2)

105Pa ＝ 1.0197kgf / cm2

9. 着色度*

光学玻璃从紫外线到可视区域的吸收端在长波长一侧（可视区域）上几乎找不到吸收、所以可以使用着色度简便地表示其分光透射特性。 使用研磨成10±0.1mm厚度地玻璃、波长区域中的分光透过率（包括表面反射损失）、分别以λ80、λ5 表示透射率为80%和5%的波长、以5nm为单位表示着色度。 例如显示出80%透射率的波长为327nm、5%透射率的波长为285nm的玻璃的着色度表示为λ80=325，λ5=285。

図1 着色度的表示法（例）

关于ne≧1.85的高折射率玻璃、将着色度表示变更为显示出透射率70%和5%的波长（λ70 / λ5）。 例如使用λ70表示时、应表示为（420）。

10. 内部通过率*（τ）

内部透射率（τ）是不包括射入侧及射出侧的表面反射损失的透射率、使用厚度不同的一对试料的各自表面反射损失在内的透射率的测定值、来计算的。

在本手册里280~1550nm波长范围中厚度5mm以及10mm的内部透过率分别用τ5mm以及τ10mm来表示。

这里

τ： 10mm时的内部通过率

Δd： 试料厚度差 d2 - d1

T1 ： 试料厚度d1含表面反射损失的透过率

T2 ： 试料厚度d2含表面反射损失的通过

Notes ： d1>d2

11.内部透过率的程度着色度

本手册中为了简易显示着色程度、相当与80%内部透过率的波长用λτ0.8来表示。

12.色度

色度坐标根据JIS Z8701（XYZ表色系以及X10Y10Z10表色系颜色表示方法）以及JIS Z8722（物色的测定方法）来求出。 本手册登载了D65光源的X与Y的值。

13. CCI

CCI （Color Contribution Index） 是使用ISO 6728及JIS B 7097-1986规定方法所表示的每个硝种的光透过特性。

使用10mm厚的内部透过率（波长范围： 360~680 nm，波长间隔10nm）计算得出。

详细请参照JIS 7097-1986.